UPO/8회: 두 판 사이의 차이
리버티게임>Bd3076 (→답 및 토론) |
리버티게임>Sleep (→답 및 토론) |
||
| (사용자 2명의 중간 판 6개는 보이지 않습니다) | |||
| 25번째 줄: | 25번째 줄: | ||
# N=34, M=6 (해결) | # N=34, M=6 (해결) | ||
# N=100, M=9+1 (해결) | # N=100, M=9+1 (해결) | ||
# N=1000, M=14+1 | # N=1000, M=14+1 (해결) | ||
# N=10000, M=20+3 | # N=10000, M=20+3 (해결) | ||
# N=100000, M=24+3 | # N=100000, M=24+3 (해결) | ||
# N=999999, M=29+3 | # N=999999, M=29+3 (해결) | ||
# N=20200101, M=36+5 | # N=20200101, M=36+5 (해결) | ||
edit) 문제의 난이도가 하향되었습니다. M=X+Y 꼴로 나타내어져 있는 경우, X는 제가 찾은 문자열의 최소 길이이고, 여기에 여유를 주어 X+Y까지 정답으로 인정하기로 한 경우입니다. | edit) 문제의 난이도가 하향되었습니다. M=X+Y 꼴로 나타내어져 있는 경우, X는 제가 찾은 문자열의 최소 길이이고, 여기에 여유를 주어 X+Y까지 정답으로 인정하기로 한 경우입니다. | ||
| 113번째 줄: | 113번째 줄: | ||
[https://ideone.com/fRU5Ja 링크]에 프로그램 코드 전문이 있습니다. | [https://ideone.com/fRU5Ja 링크]에 프로그램 코드 전문이 있습니다. | ||
: 맞습니다. -- {{사용자:Bd3076/서명}} 2020년 1월 26일 (일) 22:55 (KST) | : 맞습니다. -- {{사용자:Bd3076/서명}} 2020년 1월 26일 (일) 22:55 (KST) | ||
n=999999 URRRURUURRURURRUURURURUURURUR | |||
n=20200101 URRRRURURURURURUURUURRURURUURRUURURU | |||
컴퓨터가 2만5천초동안 계산했습니다. ㅡ.ㅡ | |||
[[사용자:Sleep|Sleep]] ([[사용자토론:Sleep|토론]]) 2020년 1월 27일 (월) 08:49 (KST) | |||
: 둘 다 맞습니다. 정해 코드도 유클리드 호제법을 이용합니다. 솔직히 유클리드 호제법이라는 풀이가 이렇게 짧은 시간 안에 나올 줄은 상상도 하지 못했습니다. 참고로 제가 만든 코드는 1분 안에 이 답들을 찾았던 것으로 기억합니다. 코드를 지금 못 찾고 있는데, 찾으면 올리겠습니다. -- {{사용자:Bd3076/서명}} 2020년 1월 27일 (월) 10:50 (KST) | |||
{{글 숨김|코드}} | |||
<nowiki> #include <bits/stdc++.h> | |||
using namespace std; | |||
typedef long long ll; | |||
int t; | |||
int n; | |||
string s, tmps; | |||
void track(int x, int y){ | |||
if(x==1 && y==1) return; | |||
if(x>y){ | |||
int tmp = (x-1)/y; | |||
track(x-tmp*y, y); | |||
for(int i=0; i<tmp; i++) tmps.push_back('U'); | |||
} | |||
else{ | |||
int tmp = (y-1)/x; | |||
track(x, y-tmp*x); | |||
for(int i=0; i<tmp; i++) tmps.push_back('R'); | |||
} | |||
} | |||
int h, w; | |||
vector<pair<int, int> > ans; | |||
int main(){ | |||
scanf("%d", &t); | |||
while(t--){ | |||
scanf("%d", &n); | |||
ans.clear(); | |||
s.clear(); | |||
for(int i=1; i*2<=n; i++){ | |||
if(__gcd(n, i) > 1) continue; | |||
tmps.clear(); | |||
track(n, i); | |||
if(s.size()==0 || s.size() > tmps.size()) s=tmps; | |||
} | |||
s.pop_back(); | |||
printf("string: %s\n", s.c_str()); | |||
} | |||
} </nowiki> | |||
{{글 숨김 끝}} | |||
: 위와 같은 코드를 사용하면 10초 이내에 정답을 얻을 수 있습니다. -- {{사용자:Bd3076/서명}} 2020년 1월 27일 (월) 10:56 (KST) | |||
* [[UPO|돌아가기]] | * [[UPO|돌아가기]] | ||
2020년 1월 27일 (월) 16:34 기준 최신판
UPO 8회 문제는 1일차와 2일차의 구분이 없습니다. 1회, 2회와 같은 협력 문제 형태로 진행될 것입니다.
문제[편집 | 원본 편집]
'R'과 'U'만으로 이루어진 문자열 S가 있다. 문자열 S를 이용해 격자의 일부를 만들 것이다. 방식은 다음과 같다.
- 아무 칸이나 한 칸을 선택한다.
- 문자열의 글자들을 왼쪽부터 차례대로 살펴 보면서, 3번 과정을 반복한다.
- 만약 글자가 'R'이라면, 마지막으로 선택한 칸 오른쪽에 있는 칸을 선택한다. 만약 글자가 'U'라면, 마지막으로 선택한 칸 위에 있는 칸을 선택한다.
- 모든 글자를 살펴볼 때까지 3번 과정을 반복한다.
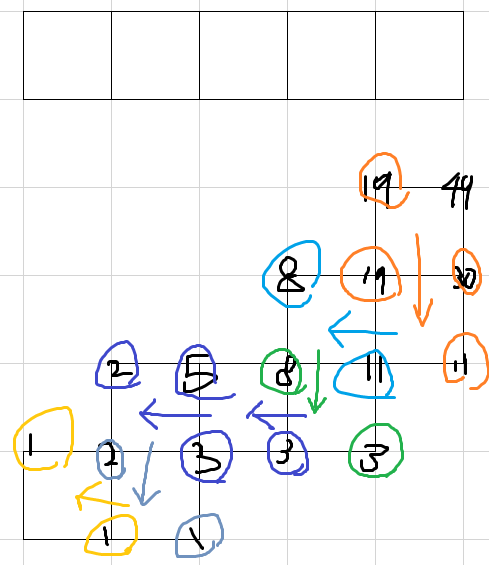
예를 들어, S="RRRR"일 때와 S="RURRURU"일 때의 격자는 아래 그림에서의 굵은 선과 같다.
문자열 S에 대한 함수 f(S)를 다음과 같이 정의하자.
- f(S)는, S를 이용해 격자를 만들 때, 격자의 맨 왼쪽 아래 꼭짓점에서 맨 오른쪽 위 꼭짓점까지 최단 거리로 이동하는 경우의 수이다.
예를 들어, f("RRRR")=6, f("RURRURU")=49이다.
우리의 목표는 f(S)=N을 만족하는 문자열 S를 찾는 것이다. 이때, S의 길이는 M 이하여야 한다. N과 M은 문제별로 주어진다. N이 같을 때, M이 작을수록 어려운 문제임에 주의하라.
- N=10, M=10 (해결)
- N=10, M=4 (해결)
- N=34, M=6 (해결)
- N=100, M=9+1 (해결)
- N=1000, M=14+1 (해결)
- N=10000, M=20+3 (해결)
- N=100000, M=24+3 (해결)
- N=999999, M=29+3 (해결)
- N=20200101, M=36+5 (해결)
edit) 문제의 난이도가 하향되었습니다. M=X+Y 꼴로 나타내어져 있는 경우, X는 제가 찾은 문자열의 최소 길이이고, 여기에 여유를 주어 X+Y까지 정답으로 인정하기로 한 경우입니다.
답 및 토론[편집 | 원본 편집]
어떤 문자열 S가 주어졌을 때 뒤에 R 혹은 U를 붙인 뒤 어떤 점화관계를 살펴볼 수 있습니다.
최종 도달지점의 왼쪽까지 가는 경우의 수를 f1(S), 바로 아래쪽까지 가는 경우의 수를 f2(S)라고 합시다.
1. f1(SU), f2(SU) 와 f1(s),f2(s)와의 관계
f2(SU)=f(S)=f1(S)+f2(S)가 성립하며 f1(SU)=f1(S) 가 성립합니다.
2. f1(SR), f2(SR)과 f1(S), f2(S)와의 관계
그림을 그리며 확인하면
f2(SR)=f2(S) f1(SR)=f(s)=f1(S)+f2(S)
가 성립합니다.
어차피 f(s)=f1(s)+f2(s)이므로
우리는 f(s)대신 f1(s) 와 f2(s)로 2가지 성분을 가지는 벡터의 점화관계를 살펴볼 수 있습니다.
아무것도 없을 때 f1(1)=1,f2(1)=1이 성립하고
문자열 뒤에 R을 붙이는 것은 성분이 각각
1 1
0 1 인 2*2 행렬을 곱하는 것이며
문자열 뒤에 U를 붙이는 것은 성분이 각각
1 0
1 1
인 2*2 행렬을 곱하는 것과 같습니다.
Sleep (토론) 2020년 1월 24일 (금) 20:10 (KST)
- 좋은 접근입니다. 참고로 정해는 매우 아름답습니다. 참고하세요. -- Bd3076 (토론) (둘러보기)기여 횟수:
만든 게임: Bd3076의 게임 2020년 1월 24일 (금) 21:11 (KST)
n=10 일때 RRUU n=34 일때 RURURU 뭔가 피보나치 수열과 관련이 있을 듯 싶은데... Sleep (토론) 2020년 1월 25일 (토) 18:27 (KST)
- 1, 2, 3번 해결하셨습니다. -- Bd3076 (토론) (둘러보기)기여 횟수:
만든 게임: Bd3076의 게임 2020년 1월 25일 (토) 20:03 (KST)
gcd(f1(s),f2(s))=gcd(f1(sr),f2(sr))=gcd(f1(su),f2(su)) 가 성립합니다.
전체적인 과정이 유클리드 호제법과 연관이 있을 것 같군요.
서로소인 두 수 a,b가 주어졌을 때
호제법을 하며 발생한 몫의 총합 : m이 되고
n=a+b값이 됩니다.
그러면 거꾸로 n으로 부터 a,b값을 추측한 뒤 m값을 검정하는 방법으로 나아가야 할 것 같습니다.
Sleep (토론) 2020년 1월 25일 (토) 23:39 (KST)
간단한 프로그래밍을 통해 확인하면
n=100일때 URRUUURUR가 나옵니다. 외부 링크Sleep (토론) 2020년 1월 26일 (일) 20:08 (KST)
- 맞습니다. -- Bd3076 (토론) (둘러보기)기여 횟수:
만든 게임: Bd3076의 게임 2020년 1월 26일 (일) 19:27 (KST)
n=1000 URUURURUURUURR
n=10000 URRRURRRURRURUURURUU
n=100000 URURRURURRURRUUURRURURUR
Sleep (토론) 2020년 1월 26일 (일) 21:55 (KST) 링크에 프로그램 코드 전문이 있습니다.
- 맞습니다. -- Bd3076 (토론) (둘러보기)기여 횟수:
만든 게임: Bd3076의 게임 2020년 1월 26일 (일) 22:55 (KST)
n=999999 URRRURUURRURURRUURURURUURURUR
n=20200101 URRRRURURURURURUURUURRURURUURRUURURU
컴퓨터가 2만5천초동안 계산했습니다. ㅡ.ㅡ Sleep (토론) 2020년 1월 27일 (월) 08:49 (KST)
- 둘 다 맞습니다. 정해 코드도 유클리드 호제법을 이용합니다. 솔직히 유클리드 호제법이라는 풀이가 이렇게 짧은 시간 안에 나올 줄은 상상도 하지 못했습니다. 참고로 제가 만든 코드는 1분 안에 이 답들을 찾았던 것으로 기억합니다. 코드를 지금 못 찾고 있는데, 찾으면 올리겠습니다. -- Bd3076 (토론) (둘러보기)기여 횟수:
만든 게임: Bd3076의 게임 2020년 1월 27일 (월) 10:50 (KST)
코드
- 위와 같은 코드를 사용하면 10초 이내에 정답을 얻을 수 있습니다. -- Bd3076 (토론) (둘러보기)기여 횟수:
만든 게임: Bd3076의 게임 2020년 1월 27일 (월) 10:56 (KST)